Ecological Synchrony
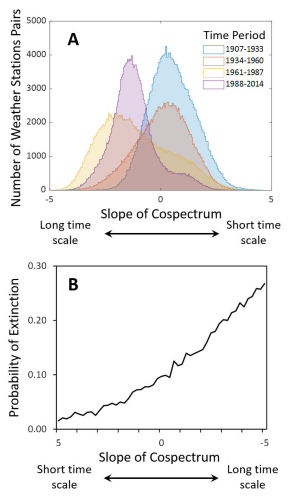My colleagues and I are using spectral analyses to examine synchrony in the frequency domain. Our goals are (1) to derive new theoretical results, (2) to conduct new laboratory experiments that test our theoretical predictions, and (3) to analyze data from ecological and environmental databases that extend over large geographical areas and extended periods of time. Our results show how total synchrony changes in response to population growth rates, rates of dispersal among populations, and the time scales of environmental variation and environmental correlation. We also found that time scales of environmental correlations are becoming longer, perhaps due to climate change, and that these changes impose an increased risk of extinction for fragmented ecological populations.
Climate change may increase extinction risk for fragmented populations. (A) Distribution of slopes of cospectra of mean annual temperatures for 175,154 paired US weather stations. (B) Probability of extinction of populations increases as the time scale of environmental correlation increases.
Spectral Analyses of Population Dynamics
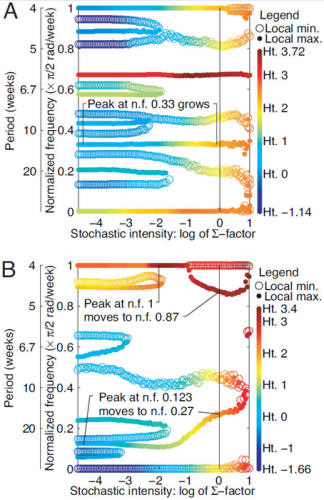The power spectrum is a powerful mathematical tool that takes a population time series as input and gives as output a plot showing the amount (power) of fluctuation that occurred in the population at each of a range of frequencies. Frequencies at which important oscillations occurred can be read from this plot; they are the frequencies at which peaks in the spectrum occur. The spectrum gives a comprehensive signature of population dynamics. We use controlled laboratory experiments and mathematical models to understand the interaction between environmental variability and intrinsic population nonlinearities. Our findings contribute to understanding how nonlinear population dynamics interact with stochasticity.
Spectral peaks and valleys with increasing intensity of stochasticity in the LPA) model parameter values for a 3-cycle (A) and a 2-cycle (B). One can see how stochasticity interacts with the nonlinear deterministic dynamics to cause a shift in the frequencies of some spectral peaks while other peaks are intensified or eliminated.
Nonlinear Population Dynamics
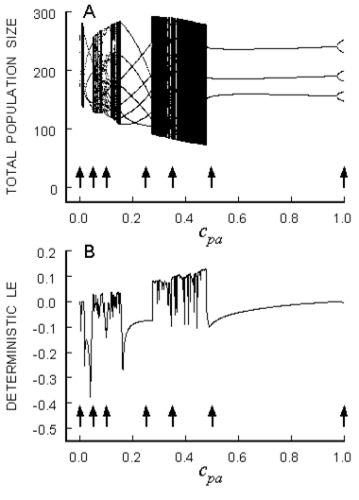I participate in an interdisciplinary research project that integrates mathematical, statistical, and experimental methods for the investigation of nonlinear population dynamics. Our goal is to provide experimental tests of dynamic behaviors such as periodic cycles, aperiodic orbits, multiple attractors, unstable equilibria with stable and unstable manifolds, chaos, and strange attractors. Laboratory populations of flour beetles of the genus Tribolium are serving as an animal model. For example, we reported an experiment that provided the first convincing example of chaos in ecology. This work also focuses on how stochasticity interacts with nonlinearity to influence population time series.
Transitions in predicted deterministic dynamics for the point estimates of the LPA model. (A) the bifurcation diagram and (B) deterministic Liapunov exponents. Arrows indicate experimentally fixed values of a model parameter.
Spatially-Mediated Dynamics in Benthic Communities
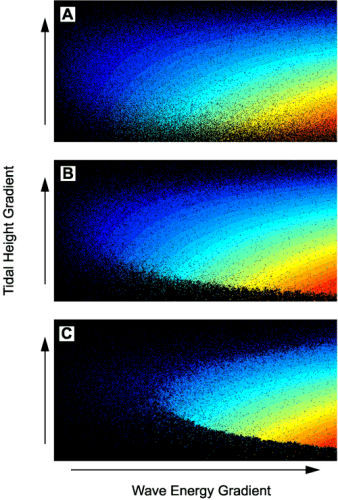I am part of a research group investigating the dynamics of size-specific predation of mussels by sea stars in rocky intertidal communities. Spatial neighborhood effects in both recruitment and predation play an important role in these dynamics and the strengths of these neighborhood effects vary over gradients of wave energy and tidal exposure. We integrate empirical data into a variety of models of the intertidal zone including stochastic cellular automata, mean field ordinary differential equations, and agent-based models. Simulations of the model generate size frequency distributions over space that can be compared to real patterns from field observations.
Output from a spatially explicit cellular automata model of a mussel bed with with spatial gradients and (A) no neighborhood effects, (B) neighborhood effects, and (C) neighborhood effects and a tenfold increase in the immigration rate of predators. Mussel biomass is color coded from red for large through blue for small.